通过圆弧的圆心及两个端点坐标，绘制圆弧的三维形状。

Introduction

起源于某同学今年打研究生数学建模竞赛。绘制飞机航迹图。
通过中心点坐标c(x,y,z)、端点坐标1p1(x,y,z)和端点坐标2p2(x,y,z)，绘制三维圆弧。
起初以为很简单，接锅后发现事情不简单。。。

Method

主要思路为：通过将圆弧端点c,p1,p2旋转到XOY平面，插值后，再旋转回原平面。

主要步骤如下：

  1. 计算c, p1, p2 三点共面的平面法向量cp
  2. 通过平面法向量cp，计算其与z轴夹角sita及旋转轴roteAxis
  3. 通过旋转轴roteAxis和sita计算旋转矩阵roteMatrix和逆向旋转矩阵roteBackMatrix
  4. 将c,p1,p2旋转到XOY平面，根据step插值得到弧线点坐标roteArc
  5. 利用roteBackMatrix将roteArc旋转到原坐标系, 得到圆弧曲线坐标arc

Code

GitHub

arc.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#!/usr/bin/python3
# -*-coding:utf-8 -*-
# Reference:**********************************************
# @Time     : 2019/9/22 20:02
# @Author   : Dorad
# @File     : arc.py
# @User     : cug_x
# @Email     : <ddxid@outlook.com>
# @Software: PyCharm

import numpy as np
from scipy.sparse.linalg import expm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def get_sita(p):
    sita = np.arccos(np.dot(np.array((1, 0, 0)), p) / np.linalg.norm(p))
    if (p[1] < 0):
        sita = np.pi * 2 - sita
    return sita


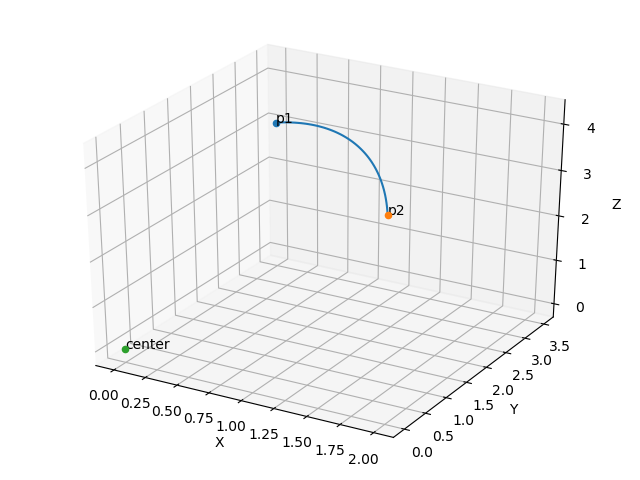
def get_arc_points(center, p1, p2, step=0.01):
    center = np.array(center)
    p1 = np.array(p1)
    p2 = np.array(p2)
    # R
    R = np.sqrt(np.sum(np.power(p1 - center, 2)))
    # get the plane, a*x+b*y+c*z=d
    cp = np.cross(center - p1, p2 - p1)
    a, b, c = cp
    d = np.dot(cp, center)
    # get the arc, need the min length
    cs = np.arccos(np.dot(p1 - center, p2 - center) / np.linalg.norm(p1 - center) / np.linalg.norm(p2 - center))
    roteAxis = np.cross(cp, [0, 0, 1])
    sita = np.arccos(np.dot(cp, [0, 0, 1]) / np.linalg.norm(cp))
    if (get_sita(cp - np.array((0, 0, 1)))) > 0:
        sita = -sita
    roteMatrix = expm(np.cross(np.eye(3), roteAxis / np.linalg.norm(roteAxis) * sita))
    roteBackMatrix = expm(np.cross(np.eye(3), roteAxis / np.linalg.norm(roteAxis) * (-sita)))
    P = np.vstack((center, p1, p2))
    RP = np.dot(P, roteMatrix)
    sp1 = get_sita(RP[1, :] - RP[0, :])
    sp2 = get_sita(RP[2, :] - RP[0, :])
    if np.abs(sp1 - sp2) > np.pi:
        st = np.hstack((np.arange(sp1, 2 * np.pi, step), np.arange(0, sp2, step))) if sp1 > sp2 else np.hstack(
            (np.arange(sp2, 2 * np.pi, step), np.arange(0, sp1, step)))
    else:
        st = np.arange(sp1, sp2, step) if sp2 > sp1 else np.arange(sp2, sp1, step)
    arc = np.array((R * np.cos(st) + RP[0, 0], R * np.sin(st) + RP[0, 1], st * 0 + RP[0, 2]))
    for i in np.arange(0, arc.shape[1]):
        arc[:, i] = np.dot(arc[:, i], roteBackMatrix)
    return arc

Example

可通过下载 GitHub 上的代码使用该函数, 使用方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from arc import get_arc_points
import matplotlib.pyplot as plt
# key points of arc.
P1=[0,1,1]
P2=[1,0,1]
C=[0,0,0]
# get points of arc
arc=get_arc_points(C,P1,P2,0.01)
# show the result
fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot3D(arc[0,:],arc[1,:],arc[2,:])
ax.set_zlabel('Z')
ax.set_ylabel('Y')
ax.set_xlabel('X')
ax.scatter3D(P1[0],P1[1],P1[2])
ax.scatter3D(P2[0], P2[1], P2[2])
ax.scatter3D(C[0], C[1], C[2])
plt.show()

Others

Email: ddxid@outlook.com